Mixed Elasticity¶

Mixed Linear¶

The boundary-value problem (Strong form) for constitutive equation (58) may be stated as follows: Given body force $\rho \bm g$, Dirichlet boundary $\bar{\bm u}$ and applied traction $\bar{\bm t}$, find the displacement and pressure-like variables $(\bm u, p) \in \mathcal{V} \times \mathcal{Q} $ (here $\mathcal{V} = H^1(\Omega), \mathcal{Q} = L^2(\Omega) $ ), such that:

(146)¶\[ \begin{aligned} -\nabla \cdot \bm \sigma - \rho \bm g &= 0, \qquad \text{in $\Omega$} \\ -\nabla\cdot\bm u - \frac{p}{\bulk - \bulk_p} &= 0, \qquad \text{in $\Omega$} \\ \bm{u} &= \bar{\bm u}, \quad \text{on $\partial \Omega^{D}$} \\ \bm \sigma \cdot \bm n &= \bar{\bm t}. \qquad \text{on $\partial \Omega^{N}$} \end{aligned} \]

with $\bm n$ be the unit normal on the boundary and its weak formulation as:

(147)¶\[ \begin{aligned} \int_{\Omega}{ \nabla \bm{v} \tcolon \bm{\sigma}} \, dv - \int_{\partial \Omega}{\bm{v} \cdot \bar{\bm t}} \, da - \int_{\Omega}{\bm{v} \cdot \rho \bm{g}} \, dv &= 0, \quad \forall \bm v \in \mathcal V \\ \int_{\Omega} q \left( -\nabla\cdot\bm u - \frac{p}{\bulk - \bulk_p} \right) \, dv & = 0. \quad \forall q \in \mathcal Q \end{aligned} \]

Mixed Hyperelasticity, initial configuration¶

We can state the mixed hyperelastic strong form as follow: Given body force $\rho_0 \bm g$, Dirichlet boundary $\bar{\bm u}$ and applied traction $\bar{\bm t}$, find the displacement and pressure-like variables $(\bm u, p) \in \mathcal{V} \times \mathcal{Q} $, such that:

(148)¶\[ \begin{aligned} -\nabla_X \cdot \bm P - \rho_0 \bm g &= 0. \qquad \text{in $\Omega_0$} \\ -\frac{\partial V}{\partial J} - \frac{p}{\bulk - \bulk_p} &= 0. \qquad \text{in $\Omega$} \\ \bm{u} &= \bar{\bm u}, \quad \text{on $\partial \Omega^{D}_0$} \\ \bm P \cdot \bm N &= \bar{\bm t}. \qquad \text{on $\partial \Omega^{N}_0$} \end{aligned} \]

and by multiplying the strong form (148) by test functions $(\bm{v}, q)$ and integrate by parts, we can obtain the weak form for finite-strain incompressible hyperelasticity as: find $(\bm{u}, p) \in \mathcal{V} \times \mathcal{Q} \subset H^1 \left( \Omega_0 \right) \times L^2 \left( \Omega_0 \right)$ such that

(149)¶\[ \begin{aligned} R_u(\bm u, p) &\coloneqq \int_{\Omega_0}{\nabla_X \bm{v} \tcolon \bm{P}} \, dV - \int_{\Omega_0}{\bm{v} \cdot \rho_0 \bm{g}} \, dV - \int_{\partial \Omega_0}{\bm{v} \cdot \bar{\bm t}} \, dA = 0, \quad \forall \bm{v} \in \mathcal{V}, \\ R_p(\bm u, p) &\coloneqq \int_{\Omega_0} q \cdot L J \, dV = 0, \quad \forall q\in \mathcal{Q}, \end{aligned} \]

where $L = -V' - \frac{p}{\bulk - \bulk_p} $. This equation contains material/constitutive nonlinearities in defining $\bm{S}(\bm{E})$, as well as geometric nonlinearities through $\bm{P} = \bm{F}\, \bm{S}$, $\bm{E}(\bm{F})$, and the body force $\bm{g}$, which must be pulled back from the current configuration to the initial configuration.

Newton linearization¶

As explained in Newton linearization, we need the Jacobian form of the (149) which is: find $(\diff \bm{u}, \diff p) \in \mathcal{V} \times \mathcal{Q}$ such that

(150)¶\[ \begin{aligned} \int_{\Omega_0} \nabla_X \bm{v} \tcolon \diff \bm{P} dV &= -R_u, \quad \forall \bm{v} \in \mathcal{V}, \\ \int_{\Omega_0} q \cdot \left( \diff L J + L \diff J \right)dV &= -R_p, \quad \forall q \in \mathcal{Q} \end{aligned} \]

where

(151)¶\[ \begin{aligned} \diff \bm{P} &= \diff \bm{F}\, \bm{S} + \bm{F} \diff \bm{S}, \\ \diff L J + L \diff J &= J \frac{\partial L}{\partial \bm{E}} \tcolon \diff \bm{E} + J \frac{\partial L}{\partial p} \diff p + L \frac{\partial J}{\partial \bm{E}} \tcolon \diff \bm{E} \end{aligned} \]

with $\diff \bm{F}$ and $\diff \bm E$ defined in (112). The linearization of the second equation of (151) is

(152)¶\[ \begin{aligned} \diff L J + L \diff J &= \left( -V^{''} \diff J - \frac{\diff p}{\bulk - \bulk_p} \right) J + L J (\bm{C}^{-1} \tcolon \diff \bm{E}), \\ &= \left( - J^2 \, V^{''} - J \, V' - J \frac{p}{\bulk - \bulk_p} \right) \bm{C}^{-1} \tcolon \diff \bm{E} - J \frac{\diff p}{\bulk - \bulk_p} \end{aligned} \]

The linearization of the second Piola-Kirchhoff stress tensor, $\diff \bm{S}$, depends upon the material model and derived below for different hyperelastic materials.

Note

For the fully incompressible case, we can set $\nu=0.5$ which leads to infinite bulk modulus. Therefore, all terms in residual (149) and jacobian (150) with coefficient $\frac{1}{\bulk -\bulk_p}$ goes to zero in the numerical implementation. In face we have

\[ L = -V', \\ \diff L J + L \diff J = \left( - J^2 \, V^{''} - J \, V' \right) \bm{C}^{-1} \tcolon \diff \bm{E}, \]

which leads to a saddle point system $\begin{bmatrix} \bm A & \bm B \\ \bm C & \bm 0 \end{bmatrix}$.

Mixed Hyperelasticity, current configuration¶

Similar to what we have shown in (117), we can write the first equation of (149) in the current configuration (see (118) ) which yields to the Jacobian form

(166)¶\[ \begin{aligned} \int_{\Omega_0} \nabla_x \bm{v} \tcolon \left( \diff \bm{\tau} - \bm{\tau} \left( \nabla_x \diff \bm{u} \right)^T \right) dV &= -r_u, \quad \forall \bm{v} \in \mathcal{V}, \\ \int_{\Omega_0} q \cdot \left( \diff L J + L \diff J \right)dV &= -r_p, \quad \forall q \in \mathcal{Q} \end{aligned} \]

where the second equation is similar to (150) and we can use (124)

\[ \diff\bm\tau - \bm\tau\left( \nabla_x \diff\bm u \right)^T = \left( \nabla_x \diff\bm u \right) \bm\tau + \bm F \diff\bm S \bm F^T. \]

to compute the linearization of the first equation in current configuration for different material models.

Perturbed Lagrange-multiplier method¶

In the previous sections we introduced the strong form of general mixed formulation for small and finite strain and by considering test functions $(\bm v, q)$ as derived in (147) and (149). Alternatively, we can derive the mixed $\bm u- p$ weak formulation based on minimization of two fields functional $\Pi(\bm u, p)$, which it is known as the perturbed Lagrangian approach. For the mixed linear case, we can write

(174)¶\[ \begin{aligned} \Pi (\bm u, p) &= \int_{\Omega} \left[ \mu \, \bm \varepsilon_{\text{dev}} \tcolon \bm \varepsilon_{\text{dev}} - p\, \trace \bm \varepsilon + \frac{\bulk_p}{2} \left(\trace \bm \varepsilon \right)^2 - \frac{p^2}{2 (\bulk-\bulk_p)} \right] \, dv - \Pi_{\text{ext}} (\bm u) \\ \Pi_{\text{ext}} (\bm u) &= \int_{\Omega}{\bm{u} \cdot \rho \bm{g}} \, dv + \int_{\partial \Omega}{\bm{u} \cdot \bar{\bm{t}}} \, da \end{aligned} \]

and by invoking the stationarity of $\Pi$ with respect to $\bm u$ and $p$, we obtain

(175)¶\[ \begin{aligned} \int_{\Omega} \nabla \delta \bm u \tcolon \left[ 2 \mu \, \bm \varepsilon_{\text{dev}} + \left(\bulk_p \trace \bm \varepsilon - p \right) \bm{I} \right] \, dv - \bm L_{\text{ext}}(\delta \bm u) &=0, \\ \int_{\Omega} \delta p \left( -\trace \bm \varepsilon - \frac{p}{\bulk-\bulk_p} \right) \, dv &= 0, \end{aligned} \]

where $\bm L_{\text{ext}}(\delta \bm u) = \int_{\Omega}{\delta \bm{u} \cdot \rho \bm{g}} \, dv + \int_{\partial \Omega}{\delta \bm{u} \cdot \bar{\bm{t}}} \, da$, and $\delta \bm u$ and $\delta p$ are virtual displacement and pressure and can be seen as the test functions $\bm v, q$, i.e., $\delta \bm u = \bm v, \, \delta p = q$. It is clear that the weak form (175) agrees with what we obtained in (147). However, the hyperelastic weak form (149), can not be derived by minimizing any functional and its linearization is not symmetric.

To write the mixed functional $\Pi(\bm u, p)$ for hyperelastic, we need to consider the strain energy of the form

(176)¶\[ \psi \left(\bm{C} \right) = \psi_{\text{vol}}(J) + \psi_{\text{iso}}(\bar{\bm{C}}) = \frac{\bulk}{2} \left(U(J)\right)^2 + \psi_{\text{iso}}(\bar{\bm{C}}) \]

we can write a two fields energy functional as

(177)¶\[ \begin{aligned} \Pi (\bm u, p) &= \int_{\Omega_0} \left[ \psi_{\text{iso}}(\bar{\bm{C}}) - p \, U(J) - \frac{1}{2}\frac{p^2}{\bulk - \bulk_p} + \frac{\bulk_p}{2} U^2\right] \, dV - \Pi_{\text{ext}} (\bm u) \\ \Pi_{\text{ext}} (\bm u) &= \int_{\Omega_0}{\bm{u} \cdot \rho_0 \bm{g}} \, dV + \int_{\partial \Omega_0}{\bm{u} \cdot \bar{\bm{t}}} \, dA \end{aligned} \]

Finding the stationary conditions with respect to $\bm{u}$ and $p$ by taking Gateaux derivative gives the weak form

(178)¶\[ \begin{aligned} \int_{\Omega_0} \bm F \underbrace{\left( \bm{S}_{\text{iso}} + (\bulk_p U - p) \, J \, U' \, \bm{C}^{-1} \right)}_{\bm S} \tcolon \nabla_X \bm v \, dV &= L_{\text{ext}} (\bm v) \\ \int_{\Omega_0} \left(- U(J) - \frac{p}{\bulk - \bulk_p} \right) q \, dV &= 0 \end{aligned} \]

where, $L_{\text{ext}} (\bm v) = \int_{\Omega_0}{\bm{v} \cdot \rho_0 \bm{g}} \, dV + \int_{\partial \Omega_0}{\bm{v} \cdot \bar{\bm{t}}} \, dA $ and we have used

\[ \begin{aligned} \frac{\partial \psi_{\text{iso}}}{\partial \bm u} \cdot {\delta \bm u} &= \frac{\partial \psi_{\text{iso}}}{\partial \bm E} \tcolon \frac{\partial \bm E}{ \partial \bm u}{\delta \bm u} = \bm{S}_{\text{iso}} \tcolon {\delta \bm E} = \bm{S}_{\text{iso}} \tcolon \text{sym} \left(\bm F^T \delta \bm F \right) \\ \frac{\partial U}{\partial \bm u} \cdot {\delta \bm u} &= \frac{\partial U}{\partial J} \frac{\partial J}{\partial \bm u} {\delta \bm u} = U' {\delta J} = J \, U' \, \bm{C}^{-1} \tcolon \tcolon {\delta \bm E} = J \, U' \, \bm{C}^{-1} \tcolon \text{sym} \left(\bm F^T \delta \bm F \right) \end{aligned} \]

where $\delta \bm{F} = \nabla_X \delta \bm u = \nabla_X \bm v$. The Jacobian for problem (178) can be written as

(179)¶\[ \begin{aligned} \int_{\Omega_0} \nabla_X \bm{v} \tcolon \left(\bm F \diff \bm{S} + \diff \bm{F} \bm{S} \right) dV &= -R_u^{PL}, \\ \int_{\Omega_0} q \left( -\diff U - \frac{\diff p}{\bulk - \bulk_p} \right) dV &= -R_p^{PL}, \end{aligned} \]

where

(180)¶\[ \begin{aligned} \diff \bm{S} &= \diff \bm{S}_{\text{iso}} + \diff \bm{S}_{\text{vol}}^u + \diff \bm{S}_{\text{vol}}^p, \\ \diff \bm{S}_{\text{vol}}^u &= \left(\bulk_p U' \diff J \right) J U' \bm{C}^{-1} + \left(\bulk_p U - p \right) \left(\diff J \, U' \bm{C}^{-1} + J\, U^{''} \diff J \bm{C}^{-1} + J U' \diff \bm{C}^{-1} \right), \\ &= \left[\bulk_p \left( J U' \right)^2 + \left(\bulk_p U - p \right) \left( J U' + J^2 U^{''} \right) \right] \left( \bm{C}^{-1} \tcolon \diff \bm E \right) \bm{C}^{-1} \\ &+ \left(\bulk_p U - p \right) J U' \, \diff \bm{C}^{-1}\\ \diff \bm{S}_{\text{vol}}^p &= - dp J U' \, \bm{C}^{-1} \\ \diff U &= U' \diff J = J \, U' \, \bm{C}^{-1} \tcolon \diff \bm E, \end{aligned} \]

where $\diff \bm{S}_{\text{iso}}$ is derived for Neo-Hookean, Mooney-Rivlin and Ogden in (156), (159) and (162). To complete the derivation we only need $U(J)$ function with condition

\[ U(J) = 0 \quad \text{if and only if} \quad J = 1. \]

For the volumetric strain energy function of the form given in (69), if we choose $V(J) = \frac{1}{4} \left(J^2 - 1 - 2 \log J \right)$, from $\bulk V(J) = \frac{\bulk}{2} U^2(J)$, we will have

\[ U(J) = \pm \sqrt{2 V} = \frac{\sign(J-1)}{\sqrt{2}} ( \underbrace{J^2 - 1 - 2 \log J }_{A})^{1/2} \]

where the derivatives are

\[ \begin{aligned} U' &= \frac{\partial U}{\partial J} = \sign(J-1) \frac{J^2 - 1}{J \sqrt{2}} A^{-1/2}, \\ U{''} &= \frac{\partial^2 U}{\partial J^2} = \sign(J-1) \frac{1}{J^2 \sqrt{2}} \left((J^2 + 1) A^{-1/2} - (J^2 - 1)^2 A^{-3/2} \right). \end{aligned} \]

Matrix-free implementation (mixed fields)¶

Similar to Matrix-free implementation for single field, we present mathematical formulation of matrix-free method for a general Dirichlet problem for general mixed problem $\bm{R}(\bm{u}, p) = [\bm{R}_u(\bm{u}, p) ~~ \bm{R}_p(\bm{u}, p)]^T = \bm 0$: Find $(\bm u, p) \in \mathcal{V} \times \mathcal{Q} $, such that

(181)¶\[ \begin{aligned} \langle\bm{v}, \bm{R}_u(\bm{u}, p) \rangle &= \int_{\Omega_0}{\bm{v} \cdot \bm{f}_0 + \nabla \bm{v} \tcolon \bm{f}_1} \, dV = 0, \quad \forall \bm{v} \in \mathcal{V}, \\ \langle q, \bm{R}_p(\bm{u}, p) \rangle &= \int_{\Omega_0}{q \cdot \bm{g}_0 + \nabla q \tcolon \bm{g}_1 } \, dV = 0, \quad \forall q \in \mathcal{Q}, \end{aligned} \]

where the operators $\bm{f}_0, \bm{f}_1, \bm{g}_0, \bm{g}_1$ contain all possible sources in the problem i.e., $\bm{u}, \nabla \bm{u}, p, \nabla p$. It should be noted that the gradient in the (181) depends on the configuration system and it could be with respect to initial configuration $\bm{X}$ i.e., $\nabla_X \bm{v}$ (Lagrangian approach) or current configuration $\bm{x}$ i.e., $\nabla_x \bm{v}$ (Eulerian approach).

In order to solve (181) with Newton-Krylov iterative solvers we need its Jacobian form: Find $(\diff \bm{u}, \diff p) \in \mathcal{V} \times \mathcal{Q} $ such that

(182)¶\[ \begin{aligned} \langle\bm{v}, \bm{J}_u(\bm{u}, p) \diff \bm{U} \rangle &= \int_{\Omega_0}{\bm{v} \cdot \diff \bm{f}_0 + \nabla \bm{v} \tcolon \diff \bm{f}_1} \, dV, \\ \langle q, \bm{J}_p(\bm{u}, p) \diff \bm{U} \rangle &= \int_{\Omega_0}{q \cdot \diff \bm{g}_0 + \nabla q \tcolon \diff \bm{g}_1} \, dV. \end{aligned} \]

where $\diff \bm{U} = [\diff \bm{u} ~~ \diff p]^T$ and the linearization of operators $\bm{f}_0, \bm{f}_1, \bm{g}_0, \bm{g}_1$ are

\[ \begin{aligned} \diff \bm{f}_i &= \frac{\partial \bm{f}_i}{\partial \bm{u}} \diff \bm{u} + \frac{\partial \bm{f}_i}{\partial \nabla \bm{u}} \nabla \diff \bm{u} + \frac{\partial \bm{f}_i}{\partial p} \diff p + \frac{\partial \bm{f}_i}{\partial \nabla p} \nabla \diff p, \quad i=0,1 \\ \diff \bm{g}_i &= \frac{\partial \bm{g}_i}{\partial \bm{u}} \diff \bm{u} + \frac{\partial \bm{g}_i}{\partial \nabla \bm{u}} \nabla \diff \bm{u} + \frac{\partial \bm{g}_i}{\partial p} \diff p + \frac{\partial \bm{g}_i}{\partial \nabla p} \nabla \diff p, \quad i=0,1 \end{aligned} \]

Compare with governing equations derived in pervious sections for linear and large deformation, it is easy to verify that

For mixed linear elasticity described in (147) we have

\[ \begin{aligned} \bm f_0 &= -\rho \bm g, \quad \bm f_1 = \bm{\sigma}(\bm u, p), \quad \bm g_0 =-\trace \bm \varepsilon - \frac{p}{\bulk-\bulk_p}, \quad \bm g_1 = \bm 0, \\ \diff \bm f_1 &= \bm f_1(\diff \bm{u}, \diff p), ~ ~ \diff \bm g_0 = \bm g_0(\diff \bm{u}, \diff p) \end{aligned} \]

For mixed hyperelastic in initial configuration described in (149) and (150) we have

\[ \begin{aligned} \bm f_0 &= -\rho_0 \bm g, \quad \bm f_1 = \bm F \bm S, \quad \bm g_0 = L J, \quad \bm g_1 = \bm 0, \\ \diff \bm f_1 &= \diff \bm F \bm S + \bm F \diff \bm S, ~ ~ \diff \bm g_0 = \diff L J + L \diff J \end{aligned} \]

For mixed hyperelastic in current configuration derived in (166)

\[ \begin{aligned} \bm f_0 &= -\rho_0 \bm g, \quad \bm f_1 = \bm \tau, \quad \bm g_0 = L J, \quad \bm g_1 = \bm 0, \\ \diff \bm f_1 &= \diff \bm{\tau} - \bm{\tau} \left( \nabla_x \diff \bm{u} \right)^T, ~ ~ \diff \bm g_0 = \diff L J + L \diff J \end{aligned} \]

For mixed hyperelastic with variational approach in initial configuration given in (178) and (179)

\[ \begin{aligned} \bm f_0 &= -\rho_0 \bm g, \quad \bm f_1 = \bm F \bm S, \quad \bm g_0 = -{U}(J) - \frac{p}{\bulk - \bulk_p}, \quad \bm g_1 = \bm 0, \\ \diff \bm f_1 &= \diff \bm F \bm S + \bm F \diff \bm S, ~ ~ \diff \bm g_0 = -\diff {U}(J) - \frac{\diff p}{\bulk - \bulk_p} \end{aligned} \]

We solve the above mixed equations using static and quasistatic solver in Ratel as explained in elasticity static and quasistatic section. For mixed elastodynamic, we only need to add the same terms (see (142) and (143)) to the residual and jacobian of the first equation of mixed matrix-free formulation described in (181) and (182), respectively.

Note

For solving incompressible elasticity we need to use different polynomial orders for displacement and pressure fields. These polynomial orders cannot be chosen arbitrarily and must fulfill the Ladyzhenskaya–Babuška–Brezzi (LBB) or inf–sup condition to ensure stability and optimal convergence [BF12, CB93]. If we rewrite the linear weak form (147) as

\[ \begin{aligned} a(\bm v, \bm{u}) + b(\bm v, p) &= f(\bm v), \quad \forall \bm v \in \mathcal{V}^0 \\ b(q, \bm{u}) + c(q, p) &= 0, \quad \forall q \in \mathcal{Q} \end{aligned} \]

then,the inf-sup constant is computable through a set of eigenvalue problems [AR09, LMW12]: Find $\lambda \in \mathbb{R}$, $0 \neq (\bm u_h, p_h) \in \mathcal{V}_h \times \mathcal{Q}_h $, such that for all $(\bm v, q) \in \mathcal{V}_h^0 \times \mathcal{Q}_h$

(183)¶\[ \langle \bm v, \bm u_h \rangle_{\mathcal{V}_h} + b(\bm v, p_h) + b(q, \bm u_h) = -\lambda \langle q, p_h \rangle_{\mathcal{Q}_h}, \]

where $b(\bm v, p_h)$ is a bilinear form and $\langle \bm v, \bm u_h \rangle_{\mathcal{V}_h}$ is the inner product of the associated space $\mathcal{V}_h$. The Brezzi stability conditions state that there exists a unique solution for mixed problem if and only if inf-sup constant, $\beta_h = \sqrt{\lambda_{\text{min}}}$, is bounded below for all mesh size $h > 0$.

../../../../_images/mixed-element.svg — Fig. 3 2D mixed element examples with discontinuous and continuous (last column) pressure.¶

2D mixed element examples with discontinuous and continuous (last column) pressure. shows some mixed elements where the pressure DoF can be continuous or discontinuous. We performed the inf-sup analysis by solving the eigen problem (183) for various mixed elements on square $[0,1]^2$ and stretched meshes $[0,1] \times [0, 0.1]$ and displayed on Inf-sup constant for various mixed-elements with continuous (top row) and discontinuous (bottom row) pressure on square and stretched meshes.. All mixed elements with continuous pressure are inf-sup stable on element with aspect ratio 1 and 10. However, for the discontinuous pressure, the inf-sup constant for widely-used $Q_1P_0$ and $Q_nQ_{n-1}$ elements is decreasing under mesh refinement which make them unstable. Moreover, $Q_2P_1$ element which is stable on square mesh, becomes unstable on the stretched meshes. In fact, the inf-sup constant of $Q_2P_1$ is decreasing by factor $1/\sqrt{a}$ where $a$ is element aspect ratio. Thus, for stretched structure one should avoid using this element. Results exhibited below is created using the open source Julia programming language and is reproducible as given in this demo code.

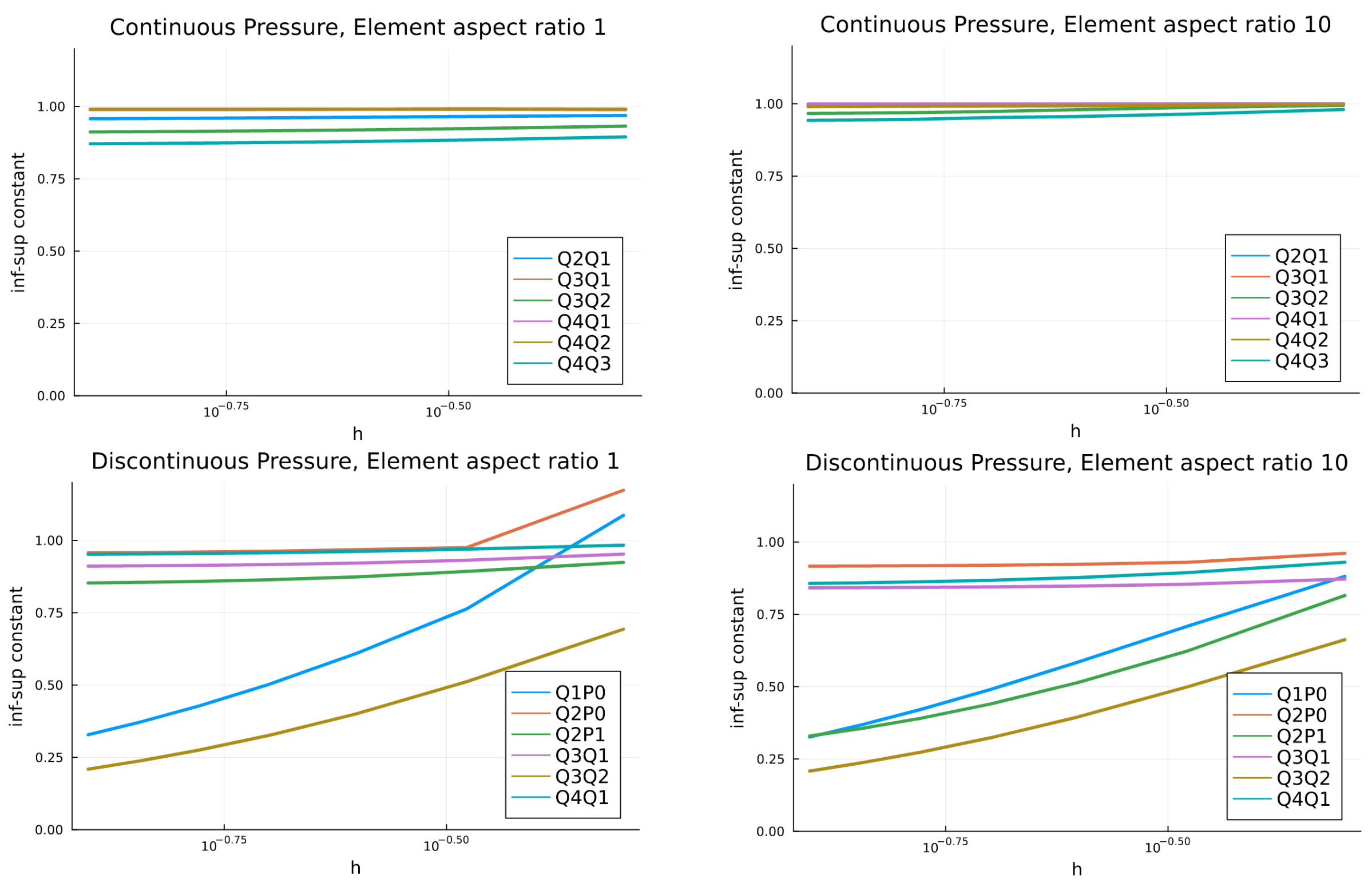
../../../../_images/inf-sup.png — Fig. 4 Inf-sup constant for various mixed-elements with continuous (top row) and discontinuous (bottom row) pressure on square and stretched meshes.¶

It should be noted element that satisfies the inf-sup condition may exhibit instability in large deformation but one should at least use the element that satisfies LBB condition for linear elasticity. To solve a system with equal-order interpolation, the mixed model must be used in conjunction with stabilization techniques like Streamline Upwind Petrov–Galerkin (SUPG) and Galerkin Least Squares (GLS).

Table 10 Mixed element Options¶
Option	Description	Default Value
`-orders [int list]`	Polynomial order of solution basis functions (displacement, pressure)
`-[prefix]_petscdualspace_lagrange_continuity` (`0` or `1`)	Enable/disable continuity of basis functions.	`1` (continuous element)
`-[prefix]__petscspace_poly_tensor` (`0` or `1`)	Enable/disable tensor product of basis functions	`1` (tensor basis)