Why Ratel

See our JOSS paper here:

Solid mechanics simulations provide vital information for many engineering applications, using a large amount of computational resources from workstation to supercomputing scales. The industry standard for implicit analysis uses assembled sparse matrices with low-order elements, typically \(Q_1\) hexahedral and \(P_2\) tetrahedral elements, with the linear systems solved using sparse direct solvers, algebraic multigrid, or multilevel domain decomposition. This approach has two fundamental inefficiencies: poor approximation accuracy per Degree of Freedom (DoF) and high computational and memory cost per DoF due to choice of data structures and algorithms. High-order finite elements implemented in a matrix-free fashion with appropriate preconditioning strategies can overcome these inefficiencies. Integrating more efficient data structures and algorithms into solid mechanics software libraries can greatly improve engineering workflows and allow users to better utilize their computational resources while new technologies like Automatic Differentiation can be used to shorten development time.

State of the field

Most finite element method (FEM) software packages for implicit analysis have limited performance due to the centrality of assembled sparse matrices, which limit performance to less than 2% of peak floating point operations per second (FLOPs) due to low arithmetic intensity (FLOP per byte of memory transferred from memory) [WWP09], rendering performance limited by memory bandwidth. Modern hardware architectures, including GPUs, favor algorithms with an intensity of 10 FLOP/byte or more [Rup20], while sparse matrices have intensities of less than 0.25 FLOP/byte. Matrix-free methods deliver higher performance than assembled matrices at both high- and low-order ([BBB+22], [KFM+21], [ABB+21a], and [MBP14]). Additionally, users who want to run their applications on High Performance Computers (HPC) are limited by the underlying requirement to write backend (hardware) specific code since different chips have different libraries needed to interface with the hardware; for example, NVIDIA devices require the use of [CUD21] while AMD GPUs require [HIP21]. Users who wish to run their code on different hardware must take the time to ensure that their code is compatible with the all of the targeted hardware, significantly increasing code development time.

MFEM [AAB+21] and deal.ii [ABD+21] are two libraries with some comparable features. In contrast to MFEM, Ratel does not currently offer the ability for users to customize the formulation of the material models past the parameters; however, Ratel offers a growing material point method capability and focuses on delivering high performance with libCEED’s code generation GPU backends. In contrast to deal.ii, Ratel uses C99 and code generation for performance over C++ templates, in an effort to provide error messages that are easier to debug. Also, Ratel has more robust and mature GPU support than deal.ii.

Abaqus [Aba25] is another widely used commercial package with comparable features. Developing constitutive models requires tensor derivatives of nonlinear scalar functions. In Abaqus, extensions through UMAT or UHYPER interfaces are typically implemented via manual derivation and coding of these derivatives, following solver-specific conventions that can be error-prone and, in some cases, lead to instabilities [SGTB24]. While it is possible to integrate external automatic differentiation (AD) tools such as Enzyme or ADOL-C into UMAT implementations, doing so generally requires additional setup and expertise. However, Ratel addresses this by leveraging automatic differentiation (AD) to compute exact derivatives directly from a nonlinear strain energy function, providing first derivatives for constitutive modeling and second derivatives for the consistent tangent.

Statement of need

Ratel is a solid mechanics library that provides material models and boundary conditions that utilize the high-order matrix-free capabilities of libCEED ([ABB+21b], [BAB+21]) and the linear and non-linear solvers from PETSc ([BAA+25], [ZBB+21]). Ratel supports both FEM and implicit material point method (iMPM) implementations ([CAB+20a], [MDMuhlhaus03]), allowing users to select their method of choice at run-time. Ratel has an extensible materials library that includes finite-strain hyperelastic, elastoplastic, viscoelastic, poroelastic, and fracture models, including stable mixed formulations for near-incompressible regimes. These models are written in C99 and only contain code syntax also supported by CUDA and HIP. Because libCEED lets users write hardware-agnostic code, Ratel users can run solid mechanics simulations with any libCEED-supported backend, selecting between CPUs or GPUs at runtime.

Ratel users can take advantage of all the packages and algorithms supported by PETSc, including Hypre [FLSjogreen+21] and Kokkos [TLGA+22]. Ratel accepts runtime arguments as command-line flags and/or YAML format, providing users the flexibility to use different libCEED backends, PETSc solvers and preconditioners, or Ratel material models easily. The performance benefits of Ratel’s approach to solid mechanics is explored in [BBB+22].

Concepts and interface

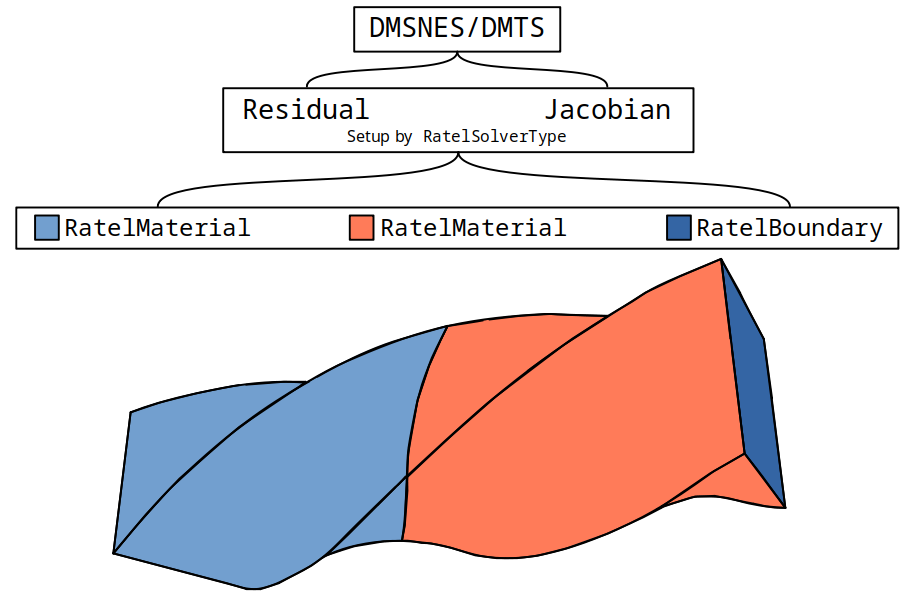
The role of Ratel is to properly set up a PETSc domain management (DM) object representing the mesh for the user’s prescribed solid mechanics simulation and create the libCEED operators to compute the non-linear residual evaluations for PETSc time-steppers (TS) and non-linear solvers (SNES) as well as the Jacobian evaluations for PETSc linear solvers (KSP), as well as any ancillary operators for solution postprocessing. libCEED provides performant implementations of these operators on the targeted hardware (\autoref{libCEEDBackends}). These libCEED operators are attached to the DM’s non-linear solver context (DMSNES) or time-stepper context (DMTS) which configures the user’s selected solver with the appropriate function callbacks to run the user’s simulation.

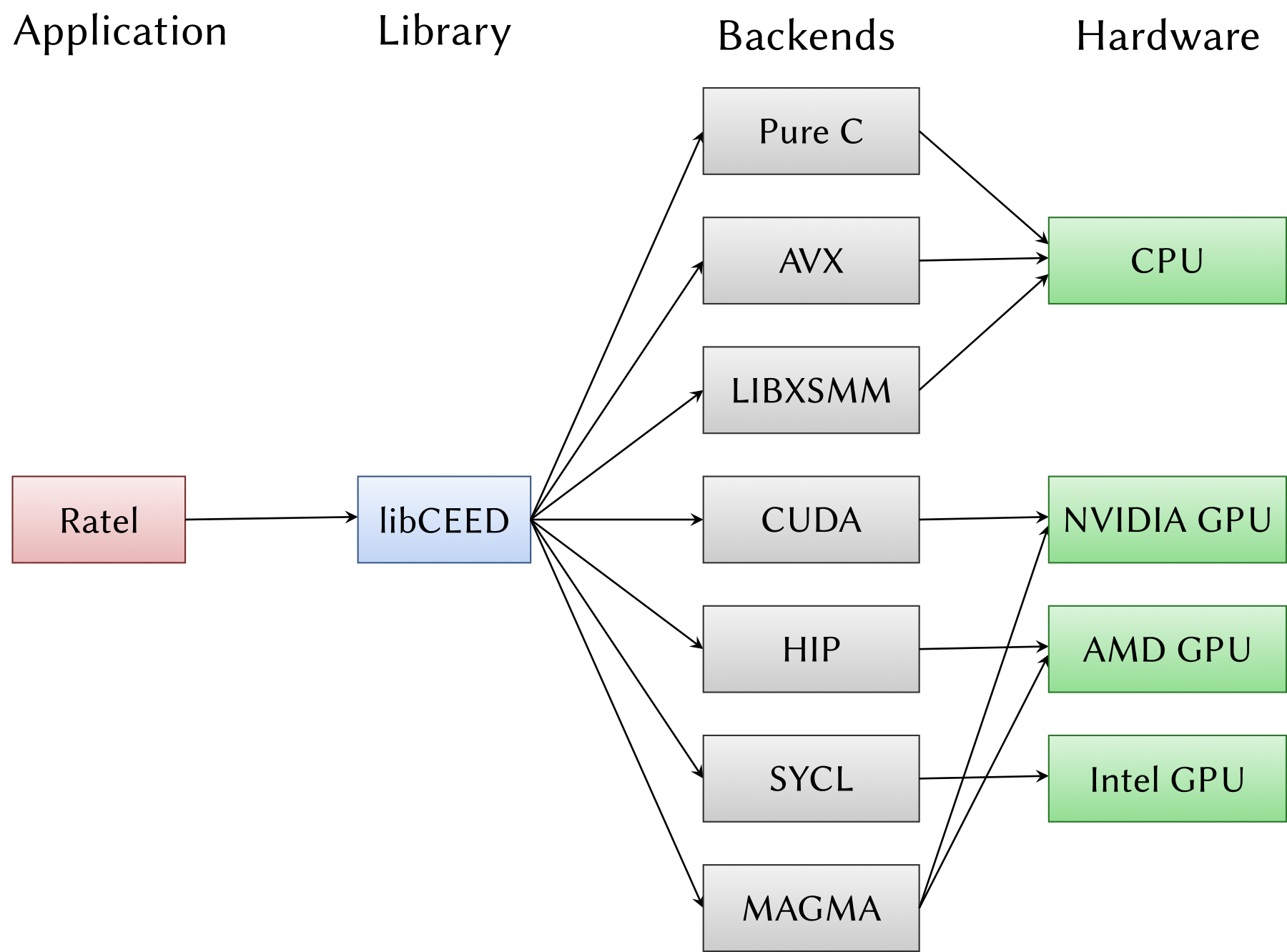
Ratel currently only uses Continuous Galerkin finite elements; however other types of finite elements supported by PETSc and libCEED could be added in the future.

Ratel is organized around RatelMaterial objects, separate material regions in the domain (\autoref{internalAPI}). Each RatelMaterial is responsible for adding volumetric terms to the residual and Jacobian operators as well as any surface terms that require volumetric or material model values. Additionally, each RatelMaterial is responsible for building and configuring corresponding preconditioner components, as needed. Users can configure RatelMaterials at runtime, identifying the material parameters and mesh regions on which to apply use each material.

Boundary and forcing terms that do not require volumetric or material model parameters, such as Dirichlet boundary conditions, are handled separately from RatelMaterial. RatelBoundary objects can also be specified at runtime.

Material models and boundary conditions

Similar to other FEM packages, Ratel provides users with several material models to use in simulations such as linear elasticity, Hencky, Neo-Hookean, Mooney-Rivlin, and Ogden hyperelasticity models ([Hol00], [Hug12]), available in both compressible and incompressible limits. These models are written in a numerically stable way [SGTB24] to improve accuracy by reducing floating point errors. In addition to the elasticity models, Ratel material development can be broken up into three main categories: matrix-free implementations of complex material models, the use of automatic differentiation (AD) to simplify material model implementation, and MPM versions of material models.

Advanced material models in Ratel include a phase-field model for brittle fracture with AT1 and AT2 damage ([MHW10], [TanneLB+18], and [AMM09]), linear and finite strain von Mises plasticity ([EB90] [WA90]), and both linear (Biot’s) ([Che16], [DCC13]) and finite strain [ICR24] poroelasticity models. Ratel supports running simulations with multiple material models on different regions of a mesh.

There is also ongoing research around incorporating AD tools such as Enzyme ([MC20], [MCP+21]) and ADOL-C [WG12] into the material model development pipeline. AD allows the user to avoid the time consuming and error-prone process of calculating complex derivatives by hand for the Jacobians. There are several existing examples in Ratel demonstrating the use of both Enzyme and ADOL-C for hyperelastic material models, with ongoing work towards an AD plasticity model.

Finally, Ratel has an iMPM implementation, based on [CAB+20a] and [MDMuhlhaus03], with iMPM versions of the Neo-Hookean and damage material models. Like the FEM material models, the iMPM material models utilize the libCEED interface, allowing iMPM simulations to be run on any libCEED-supported architecture, including AMD and NVIDIA GPUs.

Ratel also provides several boundary conditions. Ratel offers two main forms of Dirichlet or essential boundaries, clamp and slip. Clamp boundary conditions are displacement-specific and constrain the entire displacement field on the face; the constrained values specify linear and rotational displacement on the face at a given point in time. Slip boundary conditions are a more general option, allowing for individual components of a field to have values prescribed. Slip boundaries allow for the specification of symmetry or linearly interpolated values.

Traction (Neumann) boundary conditions, which apply external forces on a surface are supported. Pressure boundary conditions from liquids or gases acting on the surface of the solid structure are also supported, with the load depending on the current deformation state. Finally, Ratel supports contact boundary conditions with rigid obstacles using Nitsche’s method [Mli18] either frictionless or with Coulomb or Threlfall friction models [MFPCL16]. These boundary conditions are configured via command line options and may be time varying.

Examples

Ratel is a library that can be integrated into existing applications and also provides driver applications for static, quasistatic, and dynamic simulation and analysis. Here, we demonstrate some example simulations using these drivers.

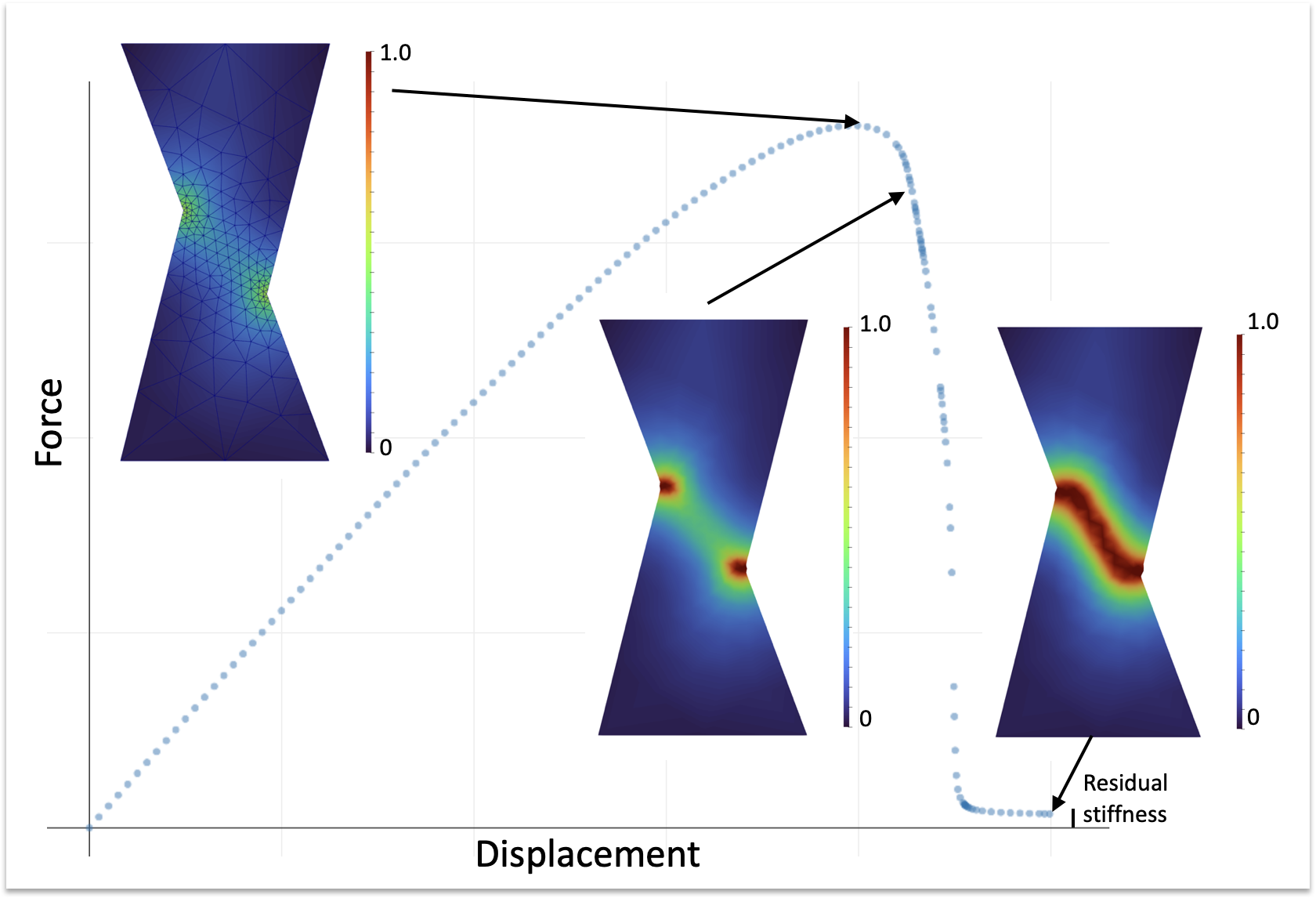
The first example is a coarse quasistatic simulation of a compressive shear test for a generic brittle material. It employs the AT2 phase-field model in a monolithic scheme, incorporating damage viscous regularization and adaptive time-stepping. This example highlights Ratel’s capability to handle advanced material models in non-trivial loading conditions.

bin/ratel-quasistatic -options_file examples/ymls/ex02-quasistatic-elasticity-linear-damage-compressiveshear-AT2-face-forces.yml

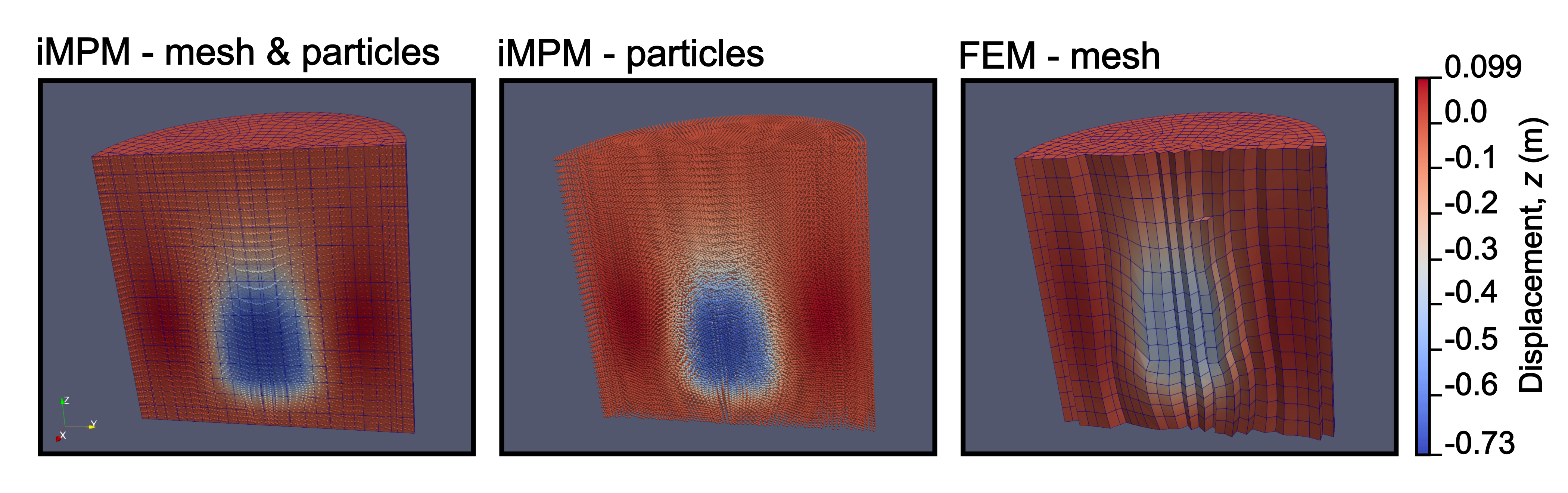
The second example is a quasistatic iMPM simulation of cylinder with a dense high-modulus inclusion surrounded by a low-density low-modulus near-incompressible “foam” (\autoref{sinker-MPM-FEM}). This simulation demonstrates Ratel’s ability to handle mixed materials and curved geometry as well as the iMPM simulation capability. Note that for the iMPM simulation there is no mesh deformation like there is in FEM simulations since only the particles move in iMPM.

bin/ratel-quasistatic -options_file examples/ymls/ex02-quasistatic-elasticity-mpm-neo-hookean-damage-current-sinker-cylinder.yml

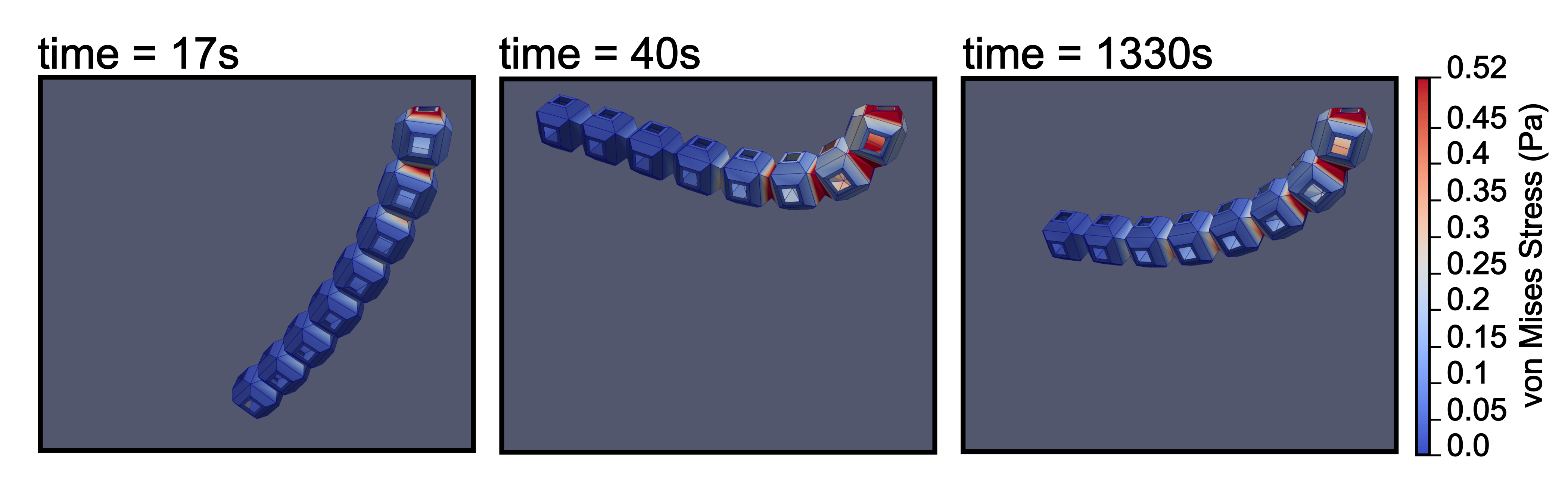
The next example is a dynamic simulation of 8 Schwarz-P cells with an applied traction force creating pendulum-like motion (\autoref{dynamic-pendulum}). Schwarz-P meshes are especially helpful in studying solver and preconditioner robustness and scaling.

bin/ratel-dynamic -options_file examples/ymls/ex03-dynamic-elasticity-schwarz-pendulum-enzyme.yml